Tai, ką mes žinome yra lašas, ko nežinome – vandenynas.
Isaacas Niutonas
Matematikos pasaulyje formulės užima svarbią vietą. Šios gerai žinomos lygtys pastebimos kiekvienoje matematinėje teoremoje nuo senųjų laikų iki naujausių XX amžiaus atradimų. Su kiekviena nauja matematine lygtimi iškyla ir daug naujų klausimų, į kuriuos atsiranda daug naujų atsakymų.
Žemiau pateikiame keletę matematinių lygčių, kurios iš esmės pakeitė mūsų pasaulio suvokimą.
Pitagoro teorema
Ši teorema, datuojama 530 m. pr. Kr., tikriausiai yra viena žinomiausių matematinių lygčių.
Jos formulė:
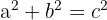
Pitagoro teorema yra viena iš moderniosios matematikos pagrindų. Ji daug prisidėjo prie matematikos, kaip disciplinos, vystymosi. Net ir po daugelio metų, šios teoremos formulė liko įsirėžusi į mūsų atmintį.
Stačiakampio trikampio įžambinės kvadratas lygus kitų dviejų kraštinių kvadratų sumai.
Dėka Pitagoro ir jo žymiosios lygties, šiandien galime lengvai apskaičiuoti ilgius, kampus ir nustatyti, ar trikampis yra status. Ši lygtis yra tik vienas iš daugelio pavyzdžių, įrodančių, kad matematika yra mūsų kasdienio gyvenimo dalis.
Pitagoro teorema iki šiandien yra naudojama tokiose praktinėse srityje kaip statybos, architektūra, darbas su mediena ir daug kitų.
Visuotinės traukos dėsnis
Visuotinės traukos dėsnis teigia, kad du kūnai Visatoje traukia vienas kitą jėga, kuri priklauso nuo jų masių ir atstumo, esančio tarp jų.
Ši jėga yra tiesiogiai proporcinga kūnų masių sandaugai ir atvirkščiai proporcinga atstumo tarp jų kvadratui.
Pavyzdžiui, Žemė traukia Mėnulį ir atvirkščiai.
Tas pats dėsnis taikomas traukai tarp obuolio ir Žemės bei tarp planetų ir Saulės: Visuotinės traukos dėsnis.
Šį dėsnį ir lygtį, kuri yra viena žymiausių, kuri kada nors egzistavo, sukūrė Izaokas Niutonas XVII amžiuje. Formulė yra tokia:
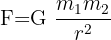
Kur:
- F: Gravitacinė jėga (N: Niutonai)
- M: Pirmojo kūno masė (dažniausiai planeta, kg)
- m: Antrojo kūno masė (kg)
- R: Atstumas tarp kūnų (metrais)
- G: Gravitacijos konstanta
Gravitacinė sąveika yra universali. Ji taikoma visų tipų materijai. Ir gravitacija pasireiškia tik kaip trauka; ji neapima kūnų atstūmimo.
Reliatyvumo teorija
Grynoji matematika tam tikra prasme yra loginių idėjų poezija.
Albertas Einšteinas
Reliatyvumo teorijos formulė tikriausiai yra viena žinomiausių lygčių. Ir vis dėlto, ne visi ją pilnai supranta.
Reliatyvumo teoriją sukūrė Albertas Einšteinas, kuris padėjo pakeisti mūsų mokslinį supratimą apie erdvės ir laiko prigimtį.
Ši teorija yra viena žinomiauisų matematinių teorijų, o jos formulė yra tokia:
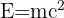
Bet ką reiškia ši formulė?
Pirmiausia, svarbu atkreipti dėmesį, kad bet kurio objekto masė yra energijos forma. Formulėje objekto masė (𝑚) gali būti paversta energija (𝐸), ir atvirkščiai. „c“ reiškia šviesos greitį ir jis yra pakeltas kvadratu, nurodant, kad net maža masės dalis gali būti paversta dideliu energijos kiekiu.
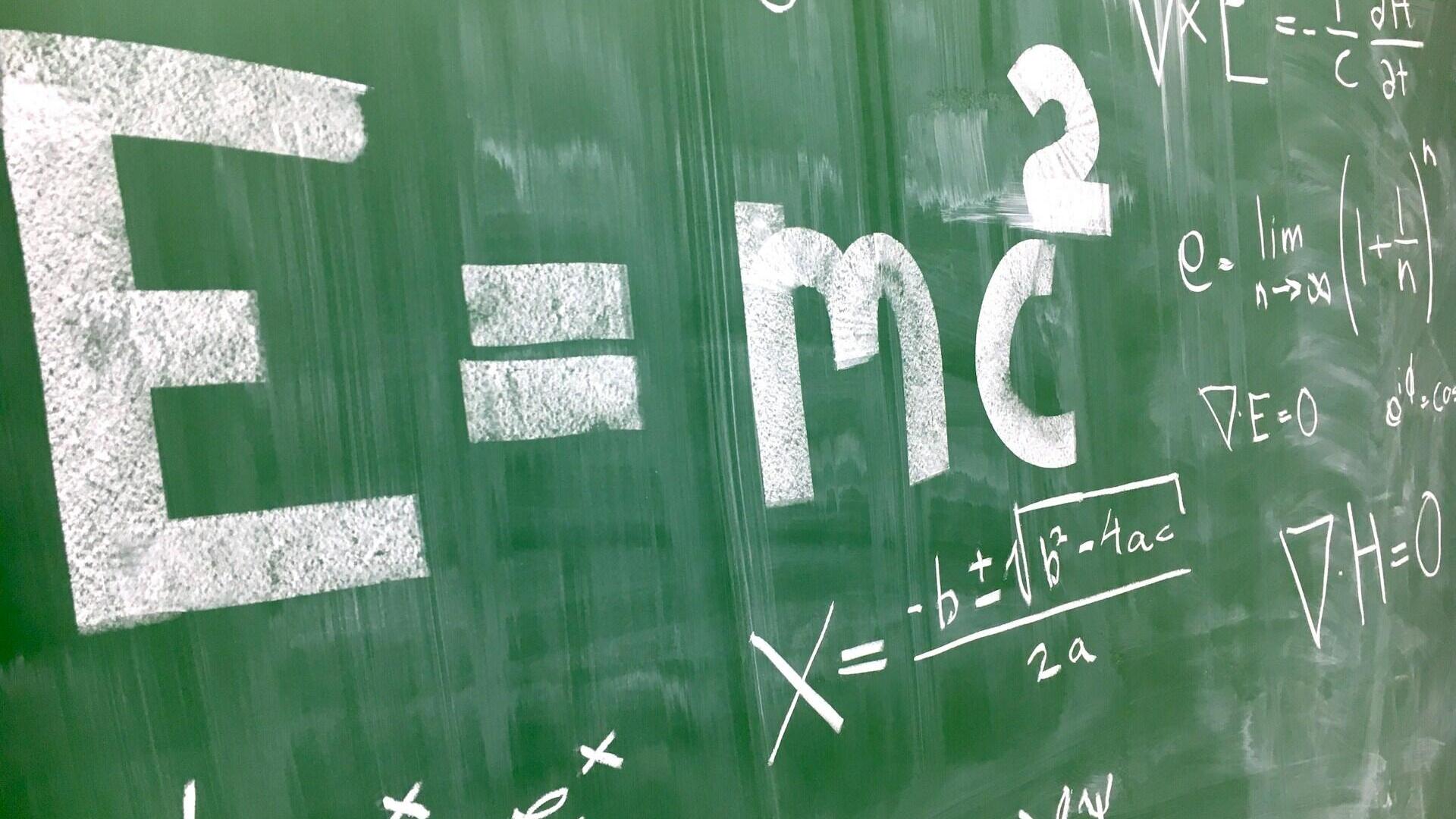
Ši formulė, iliustruojanti reliatyvumo teoriją (specialiąją ir bendrąją reliatyvumo teorijas), iš esmės pakeitė mūsų supratimą apie fiziką.
Ji išlieka aktuali ir šiandien, kadangi ji įrodo, kad materija gali virsti energija ir atvirkščiai 🤓
Specialioji reliatyvumo teorija iškėlė idėją, kad šviesos greitis yra visuotinė konstanta, kuri nesikeičia, o laiko tėkmė nėra vienoda visiems objektams – ji priklauso nuo jų judėjimo greičio.
Reliatyvumo teorija laikoma pačia garsiausia matematine teorija visame pasaulyje, kadangi ši įrodė, kokią svarbą matematika turi realiame gyvenime ir kaip ji gali pakeisti istorijos eigą.
Apskritimo plotas
Apskritimas – tai uždara plokščia kreivė, kurios visi taškai yra vienodu atstumu nuo centro. Paprastai tariant, apskritimas yra uždara linija, panaši į žiedą arba padangą.
Jo plotas apskaičiuojamas pagal formulę:
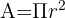
Kur 𝐴 yra apskritimo plotas.
Toliau, turime π (π = 3.1416) ir tuomet 𝑟, kuris reiškia apskritimo spindulį. Spindulys yra atstumas tarp apskritimo centro ir bet kurio jo ribos taško.
Apskritimo plotas yra svarbus tiek praktikoje, pavyzdžiui, dažant apvalų stalą, tiek fizikoje.
Šios formulės dėka galime geriau suvokti bangų reiškinius, elektromagnetinius laukus, lęšių veikimą ir net šviesos pasiskirstymą.
Chaoso teorija
Chaoso teorija – tai mokslas apie netikėtumus, nelinijinius ir nenuspėjamus reiškinius. Ji yra viena žinomiausių matematinių teorijų.
Ši teorija nagrinėja sudėtingus, nenuspėjamus procesus, tokius kaip turbulencija, orų pokyčiai, akcijų birža, smegenų veikla ir daugelis kitų. Šie reiškiniai dažnai aprašomi naudojant fraktalinę matematiką, kuri atspindi begalinį gamtos sudėtingumą.
Vienas iš žinomiausių chaoso teorijos aspektų – drugelio efektas. Jis dažnai apibūdinamas taip: drugelio sparnų plazdėjimas Australijoje gali sukelti uraganą Čilėje. Skamba kaip fantastika, tiesa? Tačiau chaoso teorija įrodo, kad tai įmanoma. Tiksliau, drugelio efektas reiškia, kad mažos pradinės sąlygos gali lemti milžiniškus pokyčius ateityje.
Mūsų gyvenimai nuolat atspindi šį principą. Kadangi negalime tiksliai žinoti visų pradinės sistemos sąlygų, todėl negalime ir tiksliai prognozuoti jos baigties. Tai galima laikyti tiesiogine priešprieša idėjai matematiką taikyti lošimuose ar pokeryje, nes net mažiausios matavimo klaidos ilgainiui gali lemti visiškai netikėtus rezultatus, palikdamos prognozę beverte. Tai – viena įdomiausių matematinių teorijų.
Eulerio tapatybė
Eulerio tapatybė išreiškiama šia lygtimi:
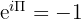
Daugelis matematikų ir ekspertų laiko šią lygtį viena įspūdingiausių, kokios kada nors buvo sukurtos.
Tai lemia ne tik jos elegancija, bet ir tai, kad ji sujungia penkias svarbias matematines konstantas į vieną formulę:
- e: natūraliųjų logaritmų pagrindas
- i: menamasis vienetas
- π: 3.1416
- 1 and 0: sveikieji skaičiai
Eulerio tapatybės grožis slypi jos paprastume.
💡 Dėl šio paprastumo ji turi didelę įtaką tokioms sritims kaip inžinerija, skaičių teorija ir kompleksinės funkcijos.
Eulierio tapatybė yra lygybė, kur e yra Eulierio skaičius, natūraliųjų logaritmų pagrindas, i yra menamasis vienetas, kuris tenkina i² = −1, o π yra pi, apskritimo ilgio ir jo skersmens santykis.
Antrasis termodinamikos dėsnis
Pirmasis termodinamikos dėsnis teigia, kad energija gali būti perduodama tarp fizinių sistemų šilumos ir darbo pavidalu. Tačiau antrasis dėsnis įveda dar vieną dydį – entropiją.
Tai – pokyčių ir evoliucijos principas, nes jis nustato, kuria kryptimi gali vykti energijos transformacijos.
Dėl šios priežasties kai kurios cheminės reakcijos yra įmanomos, o kitos – niekada neįvyks. Pavyzdžiui, jei įdėsite ledo kubelį į karštą kavą, ledas ištirps, bet kava niekada neužšals.
Antrasis termodinamikos dėsnis yra fizikinis principas, kuris apriboja šilumos perdavimo procesų kryptį tarp kūnų. Jis buvo sukurtas apibendrinus eksperimentinius faktus ir sulaukė daugybės eksperimentinių patvirtinimų.
Paprasčiau tariant, jis teigia kad neįmanoma, jog vienintelis proceso rezultatas būtų šilumos perdavimas iš šaltesnio kūno į karštesnį.
Nors prie šio dėsnio principų prisidėjo daugelis mokslininkų, didžiausią pripažinimą jis įgijo 1873 m., dėka Ludwigo Boltzmanno ir Maxo Plancko.
Pagalvokite apie ledo kubelį, įdėtą į karštos arbatos puodelį.
Kaip manote, kas nutiks?
Būtent, ledukas ištirps.
Šis dėsnis paaiškina, kodėl taip atsitinka, o ne atvirkščiai: ledas neatšaldys arbatos tiek, kad ji užšaltų.
Šrėdingerio lygtis
Ši lygtis yra viena garsiausių matematinių lygčių. Ne, šį kartą apie katę nekalbėsime – turime omenyje kitą genialią Šrėdingerio idėją, kuri jam pelnė Nobelio premiją fizikoje.
Šrėdingerio lygtis yra būtina, jei norite suprasti, kaip dalelės keičiasi bėgant laikui. Ji padeda apibūdinti įvairias būsenas, kuriose gali būti dalelė.
Ši lygtis iškelia ir įdomų filosofinį klausimą: ar materija tikrai sudaryta iš aiškių fizinių būsenų, tokių kaip kietos, skystos ar dujinės, ar egzistuoja kažkas daugiau? Kitaip tariant, ji skatina mus permąstyti materijos prigimtį ir mūsų suvokimą apie ją. Matematiniai paradoksai yra labai dažni, o ši lygtis yra raktas į atsakymus, kurie dar laukia savo atradimo.
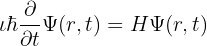
Šrėdingerio lygtis buvo itin svarbi branduolinės energijos vystymosi eigai, ji taip pat turėjo didelę reikšmę ir kompiuteriams bei lazeriams.
Dėka šios gerai žinomos lygties turėjome galimybę geriau suprasti atomų ir subatominių dalelių elgseną.
Šriodingerio lygtis paaiškina dalelės pokyčius bėgant laikui. Ji apibūdina dalelės būsenas, iš kurių galima apibūdinti bet kurią būseną.
Ši lygtis iškelia tikrą filosofinį klausimą: ar materiją sudaro galimos fizinės būsenos (kietos medžiagos, skysčiai, dujos)?
Maksvelo lygtys
Keturios Maksvelo lygtys yra vienas svarbiausių šiuolaikinės fizikos pagrindų. Jos turėjo didžiulę reikšmę tiek elektrodinamikai, tiek reliatyvumo teorijai.
Maksvello lygtys yra tokios:
Šių lygčių atradimas laikomas vienu svarbiausių pasiekimų klasikinei fizikai, nes iš jų galima išvesti visas elektromagnetizmo lygtis. Jos aprašo elektros ir magnetinių laukų sąveiką bei jų ryšį su elektriniais laukais ir krūviais. Tiek elektrinius, tiek magnetinius laukus galima pavaizduoti laukų linijų diagramomis.
Šios lygtys aiškiai parodo matematikos svarbą šiuolaikiniame pasaulyje ir įrodo, kad matematika yra neatsiejama mūsų gyvenimo dalis.
Kalbant grafiškai, abi jėgos veikia krūvius. Paprastai tariant, elektriniai ir magnetiniai laukai yra susiję – jie sąveikauja tarpusavyje ir gali būti modifikuojami.
Šios gerai žinomos lygtys stipriai prisidėjo prie matematikos plėtros. Pačios lygtys yra didelis žinių šaltinis, kuris leidžia kurti ir tobulinti kitus matematinius konceptus.
Visas šias žymias matematines lygtis sieja vienas bendras bruožas: jos yra elegantiškai paprastos, glaustos ir padeda susieti fundamentaliąją matematiką su paprastesnėmis sąvokomis. Kiekviena iš jų turi plačias bei svarbias pritaikymo galimybes tiek kasdieniame gyvenime, tiek įvairiose mokslo srityse.
Matematikos kalba yra universali. Nesvarbu, ar kalbate angliškai, prancūziškai ar ispaniškai – jei suprantate matematiką, galėsite susikalbėti bet kuria kalba.
Ar jums patiko šis straipsnis? Pasižymėkite!
Loading...
